
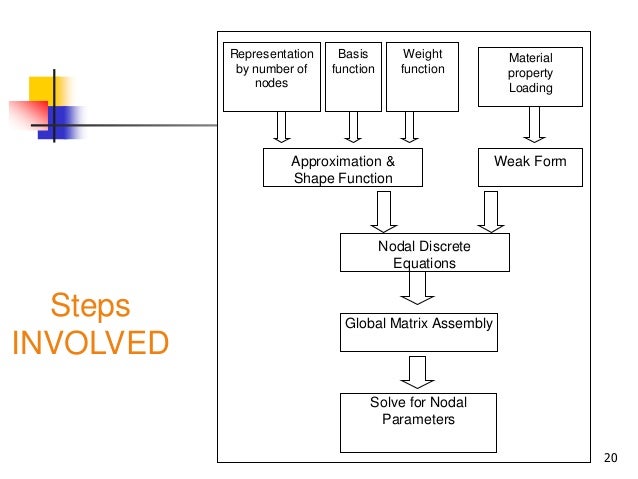
Proceedings in Applied Mathematics & Mechanics Wiley Īn innovative Space‐Time Meshfree Collocation Method (STMCM) for solving systems of nonlinear ordinary and partial differential equations by a consistent discretization in both space and time is proposed as an alternative to established mesh‐based methods. The proposed STMCM is applied to linear and nonlinear ordinary and partial differential equations of different types and its accuracy and convergence properties are studied. The key features of the proposed approach are: (i) no need to generate a mesh, (ii) simplified imposition of boundary conditions, (iii) no need to evaluate integral forms of governing equations, (iv) applicability to complex irregularly‐shaped domains. The method combines the simplicity and straightforwardness of the strong‐form computational techniques with the advantages of meshfree methods over the classical ones, especially for coupled engineering problems involving moving interfaces. A regularization technique to overcome the singularity‐by‐construction and to compute all necessary derivatives of the kernel functions is presented. the methods which do not have any underlying mesh, but work on a set of nodes only, without an a priori node‐to‐node connectivity. The STMCM belongs to the class of truly meshfree methods, i.e. Space‐Time Meshfree Collocation Method for PDEs Space‐Time Meshfree Collocation Method for PDEsĪn innovative Space‐Time Meshfree Collocation Method (STMCM) for solving systems of nonlinear ordinary and partial differential equations by a consistent discretization in both space and time is proposed as an alternative to established mesh‐based methods.


 0 kommentar(er)
0 kommentar(er)
